Анализ зубчатых механизмов. Цель работы. Кинематика планетарных и дифференциальных механизмов

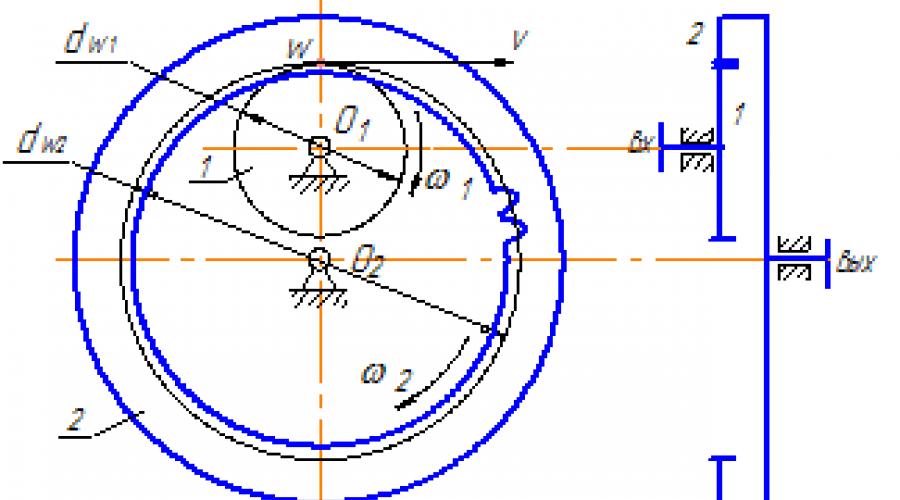
Одна пара зубчатых колес

Рисунок 35

При пересопряжении зубьев следующий зуб второго колеса должен попасть в следующую впадину первого, т.е. шаги на начальных окружностях находящихся в зацеплении колес должны быть одинаковыми:

Таким образом, для одной пары колес передаточное отношение прямо пропорционально отношению угловых скоростей и обратно пропорционально отношению чисел зубьев колес, составляющих пару:

Знак передаточного отношения показывает направление вращения колеса на выходе по отношению к направлению вращения на входе:

• (+) – направления вращения на входе и на выходе совпадают. Для пары колес направление вращения совпадает при внутреннем зацеплении (рисунок 35б);
• (–) – колеса вращаются в противоположные стороны. Это происходит при внешнем зацеплении (рисунок 35а).

На рисунке 35 дана фронтальная проекция передач, а также их условное изображение на кинематических схемах при виде сбоку (или в разрезе).

Многоступенчатая передача

Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый механизм . Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей . Схема одного из таких механизмов приведена на рисунке 36.

Рисунок 36

Запишем передаточные отношения для каждой пары колес данного механизма:

Из схемы видно, что колеса 2 и 3 находятся на одном валу и вращаются с одной угловой скоростью (ω 2 = ω 3 ), аналогично ω 4 = ω 5 . Поэтому в приведенном выше уравнении эти члены сократились.

Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:

В этой формуле “m” – число передач внешнего зацепления (если число передач внешнего зацепления четное, то знак «+», т.е. колеса на входе и на выходе вращаются в одну сторону; если нечетное, то знак «–». Количество передач внутреннего зацепления не учитывается, т.к. внутреннее зацепление не изменяет направление вращения).

В приведенном примере m=2 (пары Z 1* Z 2 и Z 3* Z 4 ; пара Z 5* Z 6 – пара внутреннего зацепления) и, таким образом, колеса «1» и «6» вращаются в одну сторону.

Планетарные и дифференциальные механизмы

В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты ). Такие механизмы называются планетарными (если имеют одну степень свободы) или дифференциальными (если степень свободы равна двум).

Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий кпд , более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.

Рисунок 37

На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо «2» имеет подвижную геометрическую ось – это и есть сателлит.

Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью . Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса «1» и «3» – иногда такие колеса называют солнечными). Звено , соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается «H»).

Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):

Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления (с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.

Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:

1. заданы ω 1 и ω 3 ; из записанной формулы определяется ω H (вариант, изображенный на рисунке 37 а);
2. заданы ω 1 и ω H ; из записанной формулы определяется ω 3 ;
3. заданы ω H и ω 3 ; из записанной формулы определяется ω 1 .

Так как звеньям можно задавать любые законы движения, то, как частный случай, одному из центральных колес зададим угловую скорость, равную нулю. Например, в рассматриваемом механизме зададим ω 3 =0 , другим словами, затормозим третье колесо. Таким приемом отнимается одна из двух степеней свободы, и механизм из дифференциального превращается в планетарный (рисунок 37 б).

Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).

Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма.

Целью кинематического анализа является определение угловых скоростей звеньев и передаточных отношений.

Передаточное отношение между звеньями a и b определяется как отношение их угловых скоростей (или частот вращения):

Угловые скорости и частоты вращения связаны соотношениями

;
.

Очевидно, что перестановка индексов у величины приводит к получению обратной величины, т.е.
.

Если оси вращения звеньев a и b параллельны, то передаточному отношению и угловым скоростямиприсваиваются знаки «+» или «-» по следующим правилам:

 любое из двух возможных направлений вращения принимают за положительное (обычно положительным считают направление вращения входного вала механизма), тогда угловая скорость каждого звена кинематической цепи приобретает вполне определенный знак;

 при одинаковом направлении угловых скоростей, входящих в (3.1), они имеют одинаковые знаки и, следовательно, определяют положительное передаточное отношение.

Рис. 3.1		Рис. 3.2

Очевидно, что для пары внутреннего зацепления (рис. 3.1) передаточное отношение

, (3.2)

а для пары внешнего зацепления (рис. 3.2) -

. (3.3)

3.1. Кинематика рядовых механизмов

Зубчатый механизм, у которого все звенья вращаются вокруг неподвижных осей, называют рядовым . Такой механизм может быть одноступенчатым (рис. 3.1 и 3.2) и многоступенчатым (рис. 3.3 и 3.4).

В многоступенчатом рядовом механизме число ступеней совпадает с числом зацеплений, его общее передаточное отношение определяют как произведение передаточных отношений всех последовательно соединенных ступеней.

Рис. 3.3		Рис. 3.4

Так, для трехступенчатого механизма по рис. 3.3 общее передаточное отношение
определится по формуле

На рис. 3.4 также представлен трехступенчатый механизм, у которого колеса
образуют соосную кинематическую цепь, причем колесоучаствует одновременно в двух зацеплениях – в одном как ведомое, в другом как ведущее (такие колеса называютсвязанными ); для этого механизма

Отметим, что при
(выходной валB вращается медленнее входного вала A ) механизм называют редуктором , а при
–мультипликатором .

3.2. Кинематика планетарных и дифференциальных механизмов

Планетарные и дифференциальные механизмы включают в себя колеса, оси которых являются подвижными. Рычаг, на котором расположены эти оси, называют водилом , а колеса с подвижными осями – сателлитами . Неподвижная ось вращения водила является центральной осью механизма. Колеса, которые вращаются или могут вращаться относительно центральной оси и при этом зацепляются с сателлитами, называют центральными или солнечными.

В планетарную ступень входят: водило; сателлиты, размещенные на этом водиле; колеса, которые зацепляются с этими сателлитами.

Рис. 3.5

На рис. 3.5 представлен простейший планетарный механизм, состоящий из водила H , центрального колеса и сателлита.

Колесо и водилоH вращаются относительно центральной оси механизма.

Сателлит совершает сложное движение, состоящее из двух вращательных: вокруг своей геометрической оси и одновременно, вместе с водилом, вокруг центральной оси механизма.

У этого механизма две степени свободы

поэтому его называют дифференциальным механизмом , или дифференциалом . Кинематику такого механизма можно описать формулой

; (3.4)

здесь
– абсолютные угловые скорости соответствующих звеньев (величины алгебраические – положительные или отрицательные),– передаточное отношениеобращенного механизма (т.е. такого воображаемого рядового механизма, который получают из заданного планетарного мысленной остановкой водила).

Из (3.4) видно, что для кинематической определимости этого механизма из трех угловых скоростей две должны быть заданы, т.е. механизм действительно является дифференциалом.

Общий вид формулы (3.4), пригодный для описания кинематики практически любого планетарного механизма, имеет вид

; (3.5)

ее называют формулой Р. Виллиса. Здесь a и b – любые два колеса одной и той же планетарной ступени, – передаточное отношение отa к b в обращенном (рядовом) механизме, это отношение всегда выражается через числа зубьев колес.

Величины угловых скоростей имогут быть любыми; в частности, при
(т.е. колесо b неподвижно) отношение
, и тогда формула Р. Виллиса приобретает вид

. (3. 6)

Формула (3.5) более универсальна и пригодна для любого планетарного механизма, тогда как (3.6) можно применять только для таких планетарных ступеней, у которых имеются неподвижные колеса (рис. 3.6 – 3.8).

Рис. 3.6	Рис. 3.7	Рис. 3.8

На рис. 3.6 показана схема редуктора Джемса с двухвенцовым сателлитом . Для него

, (3. 7)

передаточное отношение обращенной ступени

; (3. 8)

сопоставляя (3.7) и (3.8), найдем передаточное отношение редуктора

. (3. 9)

Таким же способом найдем передаточное отношение редуктора Джемса с одновенцовым сателлитом (рис. 3.7):

, (3.10)

; (3.11)

. (3. 12)

Для редуктора Давида (рис. 3.8), также имеющего неподвижное колесо в составе ступени, входным звеном является водило H , что отличает эту схему от двух других при выводе формулы для
:

; (3.13)

; (3. 14)

. (3. 15)

В этих примерах показано применение формулы Виллиса в виде (3.6), хотя было бы вполне корректным и допустимым использование ее в виде (3.5).

Все схемы по рис. 3.6 – 3.8 имеют в своем составе три центральных звена – два центральных колеса и водило; каждое из этих звеньев нагружено вращающим моментом либо от источника движения, либо от потребителя мощности (ведомого звена), либо моментом от стойки. Такие звенья называют основными и в соответствии с их видом и количеством (в данном случае – два колеса и водило) подобным схемам присвоено обозначение типа 2 KH .

Рис. 3.9

На рис. 3.9 приведена схема планетарного механизма, содержащего четыре центральных звена: три колеса – ,,и водилоH . Однако водило в этой схеме не является основным звеном, так как оно не может быть нагружено никаким внешним вращающим моментом, поэтому данный механизм отнесен к типу 3 K (т.е. символ H в обозначение типа механизма не входит).

Найдем передаточное отношение
этого механизма:

. (3.16)

Обращенный механизм для данной схемы представляет собой разветвляющуюся рядовую кинематическую цепь, каждой из двух ее ветвей соответствует свое передаточное отношение:

;
. (3.17)

После очевидных подстановок получаем

. (3.18)

Лабораторная работа №26

Кинематический анализ планетарных и дифференциальных механизмов

Цель работы: ознакомление с кинематикой планетарных и дифференциальных механизмов и определение их передаточных отношений практическим и теоретическим методом.

Объект исследования: модели планетарных и дифференциальных механизмов.

В предыдущей лабораторной работе были изучены зубчатые механизмы с неподвижными осями вращения. Отличительная особенность планетарных и дифференциальных механизмов – наличие зубчатых колес с подвижной осью вращения. На рис.1 изображен планетарный механизм. У него колесо 4 неподвижно, общая ось колес 2 и 2 ¢ вращается вместе с водилом Н вокруг колес 1 и 4, называемых солнечными. Колеса 2 и 2 ¢ называются сателлитами, а механизм – планетарным по аналогии с солнечной системой, в которой планеты, совершая оборот вокруг Солнца, вращаются также вокруг собственной оси.

У планетарного механизма степень подвижности равна единице. Если освободить колесо 4, то мы получим дифференциальный механизм, имеющий две степени свободы.

Для определения передаточного отношения планетарных механизмов применяется метод инверсии. В данном случае этот метод эквивалентен закреплению водила и освобождению неподвижного колеса.

Рис. 1

При этом мы получаем зубчатую передачу с неподвижными осями, передаточное отношение которой может быть определено по методике, изложенной в предыдущей лабораторной работе. На рис. 2 представлена схема механизма в обращенном движении. Передаточное отношение планетарного механизма обозначается буквой U , где верхний индекс указывает на неподвижное звено, а нижний индекс указывает номера входного и выходного звеньев. Для механизма на рис. 1, имеющего в качестве входного звена колесо 1, в качестве выходного водило Н , при закрепленном колесе 4. Передаточное отношение обозначается , а для обращенного механизма – .

Рис. 2

Передаточное отношение рассматриваемого планетарного механизма определяется по формуле Виллиса

где

В общем случае передаточное отношение от i -го колеса планетарного механизма к водилу при неподвижном j -ом колесе определяется формулой

Передаточное отношение дифференциального механизма (рис. 3) определяется из формулы передаточного отношения обращенного механизма

из которой следует, что дифференциальный механизм не имеет определенного передаточного отношения, если одно входное звено имеет определенную угловую скорость. Только при заданной угловой скорости двух входных звеньев (например, 1 и Н ) передаточное отношение становится определенным.

Рис. 3

Определение передаточного отношения опытным путем.

В планетарном механизме (рис. 1) поворачиваем входное звено (водило Н ) на угол φ Н =360 ° , определяем угол φ 1 поворота выходного звена (колеса 1), тогда передаточное отношение исследуемого механизма равно

Знак передаточного отношения определяется визуально.

Порядок выполнения работы

1. Ознакомиться с устройством исследуемых механизмов.

2. Заполнить приведенные ниже табл. 1, вычертив схемы исследуемого и обращенного механизмов.

Таблица 1

Планетарный механизм
Числа зубьев колес
Формула и результат определения передаточного отношения планетарного механизма
Формула и результат определения передаточного отношения обращенного механизма
Угол поворота выходного звена
Передаточное отношение, полученное опытным путем
Обращенный механизм
Числа зубьев колес
Значение и формула передаточного отношения обращенного механизма
Формула и значение передаточного отношения

Для примера рассмотрим манипулятор, изображенный на рис. 5.

Звенья механизма обозначим арабскими цифрами, количество их n = 5.

Кинематические пары, входящие в состав данного механизма:

p 5 = 3, в том числе две вращательные (А, В) и одна поступательная (С);

р 4 = 2, сферический шарнир с пальцем (Д) и цилиндрическая пара (В). До тех пор, пока захват (звено 5) не соединяется с объектом манипулирования, кинематическая цепь является незамкнутой.

Определяем степень подвижности:

W = 6  5 - 54 - 42 = 7

Таким образом, механизм имеет 7 независимых движений для ориентации и перемещения в рабочем пространстве.

После того, как захват подведен к объекту манипулирования и объединен с ним, количество подвижных звеньев становится на единицу меньше, т.е. n = 4. Число кинематических пар остается неизменным. Теперь можно определить маневренность манипулятора.

Рис. 5. Структурная схема руки манипулятора

W = 65 - 53 - 42 = 1

Тот факт, что маневренность равна единице, означает, что при фиксированном положении захвата (неподвижная точка В) звенья механизма могут менять свое положение в зависимости от положения одного из звеньев: например, при вращении звена 2 одновременно изменятся длины сторон ВД и ДЕ, а также углы треугольника ВДЕ, то есть положение звеньев 3 и 4 является функцией угла поворота звена 2.

Задача 3. Тема «Кинематический анализ зубчатых механизмов»

Задачей кинематического анализа зубчатых механизмов является определение передаточного отношения и частоты вращения выходных звеньев.

Простейшая зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. По форме колес различают цилиндрические, конические,эллептические, фигурные зубчатые передачи.

Наиболее распространены зубчатые колеса круглой формы, т. е. цилиндрические и конические. Коническая зубчатая передача осуществляет вращение между валами, геометрические оси которых пересекаются. По форме и расположению зубьев на колесе различают прямые, косые, шевронные, круговые и другие криволинейные зубья.

Постоянство передаточного отношения зубчатой передачи обеспечивается формой профиля зубьев. Наибольшее распространение получил эвольвентный профиль, так как отличается простотой изготовления (методом копирования или обкатки).

При нарезании зубчатых колес с числом зубьев эвольвентного профиля меньше некоторого предельного значения происходит подрез ножек зубьев, в результате чего прочность зубьев значительно снижается. Для устранения подрезания применяют зубчатые зацепления со смещением или так называемые корригированные зубчатые передачи.

К основным геометрическим параметрам, характеризующим зубчатое зацепление, относятся: модуль, угол зацепления, диаметры делительной, начальной и основной окружностей, коэффициент перекрытия.

Зубчатые механизмы подразделяются на механизмы с неподвижными и подвижными осями вращения.

Для выполнения кинематического анализа необходимо определить передаточное отношение зубчатой передачи.

Передаточным отношением U 1 i называется отношение угловой скорости ω 1 зубчатого колеса 1 к угловой скорости i го ω i зубчатого колеса. Вместо угловых скоростей можно использовать также понятие частоты вращения n:

U 1 i = ω 1 / ω i = n 1 / n i . (3.1)

Угловые скорости колес, находящихся в зацеплении, обратно пропорциональны радиусам начальных окружностей r w и числам зубьев колес Z.

Таким образом, передаточное отношение для пары цилиндрических колес внешнего зацепления (рис.6, а)

внутреннего зацепления (рис.6, б)

Общее передаточное отношение многозвенного механизма равно произведению передаточных отношений отдельных ступеней

U 1 i = U 12  U 23  U 34 ...U (i -1) i (3.3)

определить число ступеней в передаче;

найти передаточное отношение каждой ступени;

перемножить передаточные отношения ступеней.

Полученное число и будет передаточным отношением многоступенчатой передачи.

Механизмы с одной степенью свободы, имеющие неподвижное колесо, называют планетарными. Особенность планетарных механизмов - наличие зубчатых колес (сателлитов) с движущимися геометрическими осями.

б

Продолжение рис.6.

Механизмы с числом степеней свободы W > 2, которые обычно не имеют неподвижного колеса, называют дифференциальными.

Поскольку сателлиты в передачах с подвижными осями совершают сложное вращательное движение, то определение передаточного движения производят методом обращенного движения .

Условие. Исходные данные к задаче 3 приведены в табл.4, кинематические схемы зубчатых механизмов представлены на рис.7. Определить число степеней подвижности механизма, неизвестные числа зубьев колес и частоту вращения колес.

Схема 0 Схема 1

Схема 2 Схема3

Схема 4 Схема 5

Схема 6 Схема 7

Продолжение рис. 7

Схема 8 Схема 9

Окончание рис. 7

Таблица 4

Варианты исходных данных к задаче 3

Величина	Предпоследняя цифра шифра зачетной книжки
Z 4
Опре-делить

Зубчатые механизмы служат для передачи вращательного движения от одного вала к другому, для изменения величины и направления угловой скорости и крутящего момента.

По относительному расположению валов различают плоские и пространственные зубчатые передачи. В плоских механизмах оси вращения звеньев параллельны, и все звенья вращаются в параллельных плоскостях. В этом случае передача вращения с постоянным передаточным отношением осуществляется с помощью круглых цилиндрических колес (рис. 1).

В пространственных передачах оси вращения звеньев пересекаются (конические передачи) или скрещиваются (червячные, винтовые, спироидные и гипоидные передачи).

Различают внешнее (рис. 1.а), внутреннее (рис.1.б) и реечное зацепления.

Отношение угловой скорости ведущего вала j к угловой скорости ведомого вала k называется передаточным отношением и обозначается буквой «u» с соответствующими индексами:

Знак плюс относится к внутреннему зацеплению, а знак минус - к внешнему. Для получения больших передаточных отношений используют более сложные многоступенчатые зубчатые механизмы.,

Ступенью зубчатого механизма называется передача между двумя звеньями, расположенными на ближайших неподвижных осях. Число ступеней в зубчатых механизмах равно числу неподвижных осей без единицы.

Ступени бывают простые и планетарные. На рис. 2. А и С - простые, Б - планетарная ступени. Если скорость вращения ведомого вала меньше скорости вращения ведущего, то такой механизм называется редуктором.

Зубчатые механизмы с неподвижными относительно стойки осями колес делятся на рядовые и ступенчатые. В рядовых механизмах (рис. 3) на каждой оси насажено по одному колесу. В ступенчатых механизмах на каждой оси, кроме ведущей и ведомой, насажено по два колеса. На рис. 4. приведена схема трехступенчатого механизма. Для него

При передаче вращения коническими колесами знак передаточного отношения определяется правилом стрелок (рис. 2.5). Если стрелки на ведущем и ведомом колесах, расположенных на параллельных валах, направлены в одну сторону, то передаточное отношение будет со знаком плюс, если в противоположные стороны, то со знаком минус.

Для механизма изображенного на рис. 5.

Зубчатые механизмы, имеющие колеса, оси которых перемещаются в пространстве, называются сателлитными (рис. 2.6,а). Колеса 1 и 3, вращающиеся вокруг неподвижной центральной оси, называются центральными, а колесо 2, ось которого перемещается в пространстве, называется сателлитом. Звено Н, в котором закреплена ось сателлита 2, называется водилом.

Сателлитные механизмы с двумя и более степенями свободы называются дифференциальными, а с одной степенью свободы - планетарными.

Зависимость между угловыми скоростями звеньев может быть определена при помощи метода обращения движения. Суть его заключается в том, что всем звеньям механизма сообщается дополнительное вращение с угловой скоростью, равной по величине угловой скорости вращения водила, но противоположной по направлению (-ω н). При этом, водило мысленно останавливается и дифференциальный механизм превращается в обращенный, в котором оси всех колес неподвижны. Новые угловые скорости звеньев в обращенном движении равны

Передаточное отношение от первого звена к третьему для обращенного механизма имеет вид

Формула (4) называется формулой Виллиса, где для конкретного механизма по рис. 6,а

Задаваясь двумя скоростями, по формуле (4) можно определить третью скорость.

Заметим, что формулу Виллиса можно записать для любых двух звеньев. Например по формуле(5)

Так как ω3=0, то

В некоторых случаях целесообразно использовать комбинированные зубчатые механизмы, составленные из передач разных типов. Например, механизм, показанный на рис. 2.2, имеет две простые ступени и одну планетарную. Передаточное отношение всего механизма

В технике применяются сателлитные механизмы, состоящие из дифференциала, между ведущими звеньями которого установлена промежуточная зубчатая передача. Эта передача накладывает дополнительное условие связи, и дифференциальный механизм превращается в сложный планетарный механизм с одной степенью подвижности. Такой механизм называется замкнутым дифференциальным.